복소 지수로 표현된 신호는, 삼각 함수에 관한 오일러의 공식을 사용하여 코사인, 사인에 대해 각각 정리할 수 있다. 이것은 신호 처리에 있어서 중요한데, 주파수가 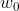 인 코사인 신호는 사실 두 개의 복소 지수 신호로 이루어져 있기 때문이다. 이 사실을 파악하기 위해, 다음의 삼각 함수에 관한 오일러의 공식을 살펴보자. 삼각 함수에 관한 오일러의 공식을 사용하여
인 코사인 신호는 사실 두 개의 복소 지수 신호로 이루어져 있기 때문이다. 이 사실을 파악하기 위해, 다음의 삼각 함수에 관한 오일러의 공식을 살펴보자. 삼각 함수에 관한 오일러의 공식을 사용하여 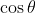 와
와 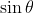 에 대해 정리하면 다음과 같다.
에 대해 정리하면 다음과 같다.
이것을 이용하여) 를 다음과 같이 양과 음의 주파수를 가진 복소 지수로 표현할 수 있다.
를 다음과 같이 양과 음의 주파수를 가진 복소 지수로 표현할 수 있다.
즉, 위의 식을 정리하면, 주파수가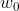 인 코사인 신호는 사실 두 개의 복소 지수 신호로 이루어져 있으며, 하나는 양의 주파수
인 코사인 신호는 사실 두 개의 복소 지수 신호로 이루어져 있으며, 하나는 양의 주파수 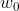 를 가지고, 다른 하나는 음의 주파수
를 가지고, 다른 하나는 음의 주파수 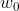 를 가진다. 양의 주파수를 가지는 복소 지수 함수의 진폭은
를 가진다. 양의 주파수를 가지는 복소 지수 함수의 진폭은 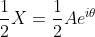 이고, 음의 주파수를 가지는 복소 지수 함수의 진폭은
이고, 음의 주파수를 가지는 복소 지수 함수의 진폭은 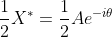 이다. 간단히 말해, 실수 코사인 신호는 서로 켤레 관계에 있는 두 개의 복소 회전 페이저의 합이다.
이다. 간단히 말해, 실수 코사인 신호는 서로 켤레 관계에 있는 두 개의 복소 회전 페이저의 합이다.
위의 과정은, 신호의 스펙트럼 성분을 얻어내는데 대단히 유용하다.
Reference
James H. McClellan, Ronald W. Schafer, Mark A. Yoder, Signal Processing First, Pearson Education, Inc, 2003
김인택, 김우식, 한승수, 서덕영 공역, Hello! 신호처리, 홍릉과학출판사, 2005, p24
이것을 이용하여
즉, 위의 식을 정리하면, 주파수가
위의 과정은, 신호의 스펙트럼 성분을 얻어내는데 대단히 유용하다.
Reference
James H. McClellan, Ronald W. Schafer, Mark A. Yoder, Signal Processing First, Pearson Education, Inc, 2003
김인택, 김우식, 한승수, 서덕영 공역, Hello! 신호처리, 홍릉과학출판사, 2005, p24