정현파(sinusoids)는 유용하기는 하지만, 이것을 직각 좌표계(cartesian coordinate)로 표현하는 것은 상당히 성가시다. 오일러의 공식을 사용하여 이것을 표기하면, 좀 더 쉽고 대수적으로 정현파를 다룰 수 있다. 또, 복소 지수 형태로 정현파를 표시하면 보다 쉽게 중요한 성분들을 구별해 낼 수 있다. 정현파는 다음과 같이 복소 지수 형태로 표시할 수 있는데, 이것은 오일러가 유도한 것이다. 자세한 것은 다음을 참고하라 : http://celdee.tistory.com/630
이로부터, 다음과 같은 식을 정의할 수 있다.
시간의 함수인 복소수를 그리려면 두 개의 그래프가 필요하다. 즉, 실수 부분과 허수 부분을 나타내는 두 개의 그래프가 필요하다. 그러나, 현실적으로는 실수 부분이 더 중요하며, 이를 위해 다음과 같은 표현을 사용한다. Re는 복소수에서 실수 부분만 취한다는 뜻이다.
이 표현은, 복소 지수 형태로 표현된 식을 쉽게 연산할 수 있을 뿐만 아니라, 이들의 중요 성분을 쉽게 파악할 수 있도록 한다. 즉, 다음과 같은 식은 단순히 지수의 합으로 계산할 수 있다.
또, 회전각) 에 대한 식이 주어졌을 때, 이 식을 복소 지수 표현에 대입하면, 회전하는 회전 페이저(rotating phasor)와 위상 변이된 페이저를 알 수 있다. 다음을 보면,
에 대한 식이 주어졌을 때, 이 식을 복소 지수 표현에 대입하면, 회전하는 회전 페이저(rotating phasor)와 위상 변이된 페이저를 알 수 있다. 다음을 보면,
이 신호는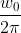 의 주기를 가지며,
의 주기를 가지며, 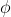 만큼 위상 변이된 신호라는 것을 쉽게 파악할 수 있다. 즉, 위의 신호는 어떤 순간
만큼 위상 변이된 신호라는 것을 쉽게 파악할 수 있다. 즉, 위의 신호는 어떤 순간  에서
에서 ) 는 진폭이
는 진폭이  이고, 각도가
이고, 각도가 ) 인 복소 지수 신호이다. 다른 복소수와 마찬가지로
인 복소 지수 신호이다. 다른 복소수와 마찬가지로 ) 도 복소 평면에서 하나의 점으로 표시되며, 반지름이
도 복소 평면에서 하나의 점으로 표시되며, 반지름이  인 원 위에 놓인다. 이 복소수는 시간의 변화에 따라 이 원 위를 회전하게 된다. 즉, 페이저
인 원 위에 놓인다. 이 복소수는 시간의 변화에 따라 이 원 위를 회전하게 된다. 즉, 페이저  에
에 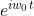 를 곱하면 고정된 페이저
를 곱하면 고정된 페이저  가 회전하게 된다. 따라서, 복소 지수 신호는 다른 말로 회전 페이저(rotating phasor)라고 부른다. 만약
가 회전하게 된다. 따라서, 복소 지수 신호는 다른 말로 회전 페이저(rotating phasor)라고 부른다. 만약 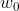 가 음수라면, 신호는 시계 방향으로 회전하고, 양수라면 시계 반대 방향으로 회전한다.
가 음수라면, 신호는 시계 방향으로 회전하고, 양수라면 시계 반대 방향으로 회전한다.
Reference
James H. McClellan, Ronald W. Schafer, Mark A. Yoder, Signal Processing First, Pearson Education, Inc, 2003
김인택, 김우식, 한승수, 서덕영 공역, Hello! 신호처리, 홍릉과학출판사, 2005
이로부터, 다음과 같은 식을 정의할 수 있다.
시간의 함수인 복소수를 그리려면 두 개의 그래프가 필요하다. 즉, 실수 부분과 허수 부분을 나타내는 두 개의 그래프가 필요하다. 그러나, 현실적으로는 실수 부분이 더 중요하며, 이를 위해 다음과 같은 표현을 사용한다. Re는 복소수에서 실수 부분만 취한다는 뜻이다.
이 표현은, 복소 지수 형태로 표현된 식을 쉽게 연산할 수 있을 뿐만 아니라, 이들의 중요 성분을 쉽게 파악할 수 있도록 한다. 즉, 다음과 같은 식은 단순히 지수의 합으로 계산할 수 있다.
또, 회전각
이 신호는
Reference
James H. McClellan, Ronald W. Schafer, Mark A. Yoder, Signal Processing First, Pearson Education, Inc, 2003
김인택, 김우식, 한승수, 서덕영 공역, Hello! 신호처리, 홍릉과학출판사, 2005