자연계를 근사하는 많은 함수 중에서 가장 중요한 것은 단연 삼각 함수이다. 왜냐하면, 삼각 함수는 원함수와 관련되어 있고, 원함수는 주기성을 가지기 때문이다. 이차 곡선 중 쌍곡선(hyperbola)도 매우 흥미로운 함수인데, 이 곡선은 원뿔을 원뿔의 밑면과 옆면 사이의 각보다 큰 각의 평면으로 자를 때 얻을 수 있다(그래서, '~을 초과하는'을 뜻하는 'hyper'가 붙었다). 그러나, 쌍곡선은 주기성을 가지지 않기 때문에 상대적으로 그 중요도가 원함수에 미치지 못한다. 나중에 밝혀진 사실이지만, 쌍곡선은 허수 주기를 가진다.
신호 처리에서는 코사인(cosine) 함수와 사인(sine) 함수를 매우 중요하게 다루며, 이들 함수를 정현파(sinusoids)라 부른다. 정현파의 일반식은 다음과 같다.
신호 처리에서, 연속적인 시간에 대한 신호를 정의할 때 변수
에 대한, 위와 같은 함수를 정의한다. 사인 함수를 사용할 수도 있지만, 본질적으로 코사인 함수와 사인 함수는 위상(phase) 차이만 있을 뿐 동일하다. 위의 식에서 
는 진폭(amplitude),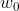 
는 라디안(radian)1으로 정의된 주파수(radian frequency), 
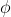는 위상 변이(phase shift)를 나타낸다. 여기서, 주파수 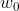와 주기(peirod) 사이에는 
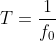의 관계가 있으며, 주기는 시간 단위로 표시된다. 진폭은 코사인 함수의 크기를 정하는 인자이며, 라디안 주파수 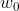로부터 
, 주기 주파수가 결정되고 단위는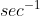 
이다. 마지막으로, 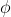는 위상 변이이며, 단위는 역시 라디안이다. 위상은 신호가 원점에서의 신호와의 간격을 나타낸다.
신호 처리에서는 코사인(cosine) 함수와 사인(sine) 함수를 매우 중요하게 다루며, 이들 함수를 정현파(sinusoids)라 부른다. 정현파의 일반식은 다음과 같다.
신호 처리에서, 연속적인 시간에 대한 신호를 정의할 때 변수
- 원의 반지름의 길이와 호의 길이가 같을 때를 1 rad으로 정한다. 따라서, 전체 원의 둘레와 360 deg로 정의된 식의 상관 관계로부터 rad 값을 알아낼 수 있다. [본문으로]