제대로 된 전역 조명을 구현하려면, 그래픽 시스템에서 제공하는 조명 처리 시스템으로는 부족하다. 더구나, 기존의 Gouraud 쉐이딩에 기반한 하드웨어 T&L 기능들은 전부 폐기 예정(deprecated)이다. DirectX는 10.0 이상에서는 아예 하드웨어 T&L 기능을 제공하고 있지 않으며, 변화가 느린 OpenGL조차 고전적인 하드웨어 T&L 관련 함수들은 폐기 예정되어 있다. 즉, 좋든 싫든 이제는 프래그먼트 프로그래밍으로 조명 효과를 구현해야 하며, 이를 위해 기존의 근사 조명식들이 어떻게 유도되었는지 알아볼 필요가 있다.
먼저, 임의의 지점에서 다음과 같이 빛이 입사되고 반사된다고 생각해보자.

여기서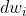 는
는 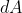 에 입사되는 빛의 단위 면적 에너지다. 즉,
에 입사되는 빛의 단위 면적 에너지다. 즉,  에 입사되는 전체 에너지량은
에 입사되는 전체 에너지량은 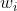 의 합으로 간주할 수 있기 때문에, 이것의 투영면을 고려한다면
의 합으로 간주할 수 있기 때문에, 이것의 투영면을 고려한다면 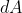 에 입사되는 에너지
에 입사되는 에너지 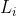 는 다음과 같다.
는 다음과 같다.
 = \frac{dE}{dw_{i}\;cos\theta_{i}})
이것을 에너지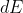 에 대해 정리하면,
에 대해 정리하면,
dw_{i}cos\theta_{i})
이 식을 적분하여 미세 에너지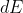 의 실제 에너지량을 구해본다면,
의 실제 에너지량을 구해본다면,
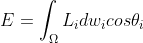
전역 조명 모델은 간단히 말해 에너지 흐름이 안정적일 때를 근사하자는 것이므로, 이 식에 의해 얻어지는 에너지가 무엇이든, 이 식은 전역 조명식에서의 쉐이딩 값을 얻어내기 위한 출발이 된다. 이제, BRDF(Bidirectional Reflectance Distribution Function)를 설명해보자. BRDF는 물체의 표면에서 빛이 어떻게 반사되는지를 설명하는 함수이다. 즉, 물체의 특정 표면에서 어떻게 빛이 이동하는지를 표현한다. 이 식에 의해 물체의 반사도, 굴절도와 같은 특성을 근사화할 수 있다. BRDF를 에너지의 관점에서 설명한다면, 들어오는 에너지와 나가는 에너지의 비라고 할 수 있다. 즉, 다음과 같이 표현할 수 있다.
 = \frac{dL_{0}(v)}{dE(l)})
여기서, 물체를 렌더링한 결과에서 관심 있는 것은 표면에서 반사되는 빛) 이며, 이 값이 물체의 색상을 결정한다.
이며, 이 값이 물체의 색상을 결정한다.
 = \int_{\Omega}f(l, v)\otimes L_{i}cos\theta_{i}dw_{i})
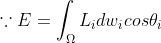
기존의 근사화된, 지역 조명식들은 점이나 방향성 광원을 대상으로 했다. 이것은, 위의 식 = \int_{W_{L}}f(l, v) \otimes L_{L}cos\theta_{i}dw_{i}) 를 근사화한 식
를 근사화한 식  \otimes E_{L}cos\theta_{i}) 에서 얻어진 것이다. 즉,
에서 얻어진 것이다. 즉, 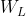 는 원래 기하 단위각을 모두 적분하여 얻어야 하는 값이지만, 이 적분 계산은 실시간 측면에서 볼 때 불가능하기 때문에 상수로 처리한다. 기존의 점광원이나 방향성 광원에서 상수화된 값을 사용하는 것은 이 근사식을 기반으로 하는 것이다. 보다 정확한 조명을 구현하기 위해서는 실제로 적절한 계산을 수행해야 한다. 다음 그림은
는 원래 기하 단위각을 모두 적분하여 얻어야 하는 값이지만, 이 적분 계산은 실시간 측면에서 볼 때 불가능하기 때문에 상수로 처리한다. 기존의 점광원이나 방향성 광원에서 상수화된 값을 사용하는 것은 이 근사식을 기반으로 하는 것이다. 보다 정확한 조명을 구현하기 위해서는 실제로 적절한 계산을 수행해야 한다. 다음 그림은 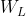 를 나타내고 있는데, 이것은 단위면적
를 나타내고 있는데, 이것은 단위면적 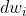 에 입사되는 에너지를 나타낸 것이다. 미세 모델로 본다면
에 입사되는 에너지를 나타낸 것이다. 미세 모델로 본다면 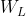 로 들어오는 모든 빛을 더해주어야 한다.
로 들어오는 모든 빛을 더해주어야 한다. 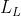 은
은 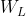 를 통해 들어오는 각각의 빛을 나타낸 것이다.
를 통해 들어오는 각각의 빛을 나타낸 것이다.

위의 식 \otimes E_{L}cos\theta_{i}) 에 의해 난반사 조명식을 설명한다면, 지역 조명에서 사용하는 난반사항은 특정한 경우에만 정확한 근사식이다. 왜냐하면, 난반사는 물체의 특정 표면에서 빛이 산란되는 현상을 나타내기 위한 것이며, 계산학적인 문제 때문에 표면에서 빛이 이동하는 현상을 모델링하는 함수인 BRDF
에 의해 난반사 조명식을 설명한다면, 지역 조명에서 사용하는 난반사항은 특정한 경우에만 정확한 근사식이다. 왜냐하면, 난반사는 물체의 특정 표면에서 빛이 산란되는 현상을 나타내기 위한 것이며, 계산학적인 문제 때문에 표면에서 빛이 이동하는 현상을 모델링하는 함수인 BRDF ) 를 상수로 처리한 것이다. 따라서, 상수로 처리된 BRDF 함수
를 상수로 처리한 것이다. 따라서, 상수로 처리된 BRDF 함수 ) 는 특정한 상황에서만 정확할 수 밖에 없다. 제대로 된 난반사된 조명값을 구하려면
는 특정한 상황에서만 정확할 수 밖에 없다. 제대로 된 난반사된 조명값을 구하려면 ) 와
와 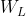 를 제대로 계산해야 한다.
를 제대로 계산해야 한다.
지역 조명 모델에서의 환경광, 난반사광, 정반사광 계산은 실시간성을 위해 위의 식의 특정 부분을 간략히 하여 근사화한 것이다. 즉, 환경광의 경우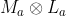 , 난반사광의 경우
, 난반사광의 경우 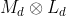 로 계산되는데, 이것은 위의 식
로 계산되는데, 이것은 위의 식  \otimes E_{L}cos\theta_{i}) 에서
에서 ) 와
와 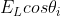 를 상수 처리한 것이다.
를 상수 처리한 것이다.
먼저, 임의의 지점에서 다음과 같이 빛이 입사되고 반사된다고 생각해보자.

여기서
이것을 에너지
이 식을 적분하여 미세 에너지
전역 조명 모델은 간단히 말해 에너지 흐름이 안정적일 때를 근사하자는 것이므로, 이 식에 의해 얻어지는 에너지가 무엇이든, 이 식은 전역 조명식에서의 쉐이딩 값을 얻어내기 위한 출발이 된다. 이제, BRDF(Bidirectional Reflectance Distribution Function)를 설명해보자. BRDF는 물체의 표면에서 빛이 어떻게 반사되는지를 설명하는 함수이다. 즉, 물체의 특정 표면에서 어떻게 빛이 이동하는지를 표현한다. 이 식에 의해 물체의 반사도, 굴절도와 같은 특성을 근사화할 수 있다. BRDF를 에너지의 관점에서 설명한다면, 들어오는 에너지와 나가는 에너지의 비라고 할 수 있다. 즉, 다음과 같이 표현할 수 있다.
여기서, 물체를 렌더링한 결과에서 관심 있는 것은 표면에서 반사되는 빛
기존의 근사화된, 지역 조명식들은 점이나 방향성 광원을 대상으로 했다. 이것은, 위의 식

위의 식
지역 조명 모델에서의 환경광, 난반사광, 정반사광 계산은 실시간성을 위해 위의 식의 특정 부분을 간략히 하여 근사화한 것이다. 즉, 환경광의 경우


