보다 나은 조명 효과를 구현하기 위해서는 전역 조명 모델을 이해해야 하며, 근본적으로 빛의 속성을 이해해야 한다. 즉, 광학(Optics)에 대한 이해가 필요하지만, 이론 물리학에서 요구하는 수준의 깊은 이해를 필요로 하는 것은 아니다.
전역 조명 모델 알고리즘의 궁극적인 목표는 어떤 장면에서 빛의 복사 에너지 방출이 안정적인 상태일 때를 최대한 근사하는 것이다. 지역 조명 모델의 환경광 / 난반사광 / 정반사광만을 사용한 근사식은 특정 상황에서만 정확한 근사식일 뿐이다. 따라서, 보다 정확한 조명을 계산하기 위해서는 아주 미세한 영역에서의 빛의 에너지를 파악해야 한다. 이를 위해서, 플럭스(flux)라고도 불리는 방사 단위를 정의하고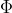 로 표기한다. 단위 면적
로 표기한다. 단위 면적 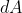 에 입사되는 빛
에 입사되는 빛  를 입사 광도(Irradiance)라 하면, 이들의 관계를 다음과 같이 표현할 수 있다.
를 입사 광도(Irradiance)라 하면, 이들의 관계를 다음과 같이 표현할 수 있다.
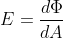
입사되는 에너지의 단위는 와트(Watt)며, 와트는 1 뉴턴의 힘을 1 m 이동하는데 필요한 에너지를 뜻한다. 즉, 위의 표현에서 단위는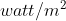 이다.
이다.
다음으로, 특정 표면에서 나오는 빛을 생각할 수 있다. 발광(radiant exitance, ) 또는 래디어시티(radiosity,
) 또는 래디어시티(radiosity,  , 확산광)로 부를 수 있는데, 이것은 입사 광도와 동일한 방법으로 측정될 수 있다. 즉, 단위 면적에서 나오는 에너지의 양으로 측정한다.
, 확산광)로 부를 수 있는데, 이것은 입사 광도와 동일한 방법으로 측정될 수 있다. 즉, 단위 면적에서 나오는 에너지의 양으로 측정한다.
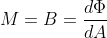
단위는 입사 광도와 동일하다.
이제, 광도(radiance)를 이야기할 수 있다. 광도란 단위 면적에서의, 기하 단위각(solid angle)에 의한 빛의 복사 에너지를 뜻한다. 기하 단위각이란 블로그지기가 임의로 생각한 단어인데, 2차원 평면에서 미분 단위 d는 굴곡이 없지만, 3차원 평면에서의 단위 면적은 굴곡을 포함할 수 있다. 따라서, 3차원 평면에서의 미분 요소 d 2차원 평면에서의 미분 요소 d와 동일한 방법으로 적분할 수 없다. 다음 그림은 이것을 나태낸 것인데, 현실적으로 는 원이 아닐 수도 있으며, 평평하게 구성되어 있지 않을 수도 있다.
는 원이 아닐 수도 있으며, 평평하게 구성되어 있지 않을 수도 있다.

즉, 특정 위치 에서
에서  가 주어진다면, 광도
가 주어진다면, 광도  은
은 ) 로 나타낼 수 있다.
로 나타낼 수 있다.  은 다음과 같이 정의된다.
은 다음과 같이 정의된다.
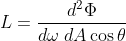
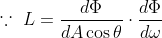
즉, 광도는 단위 면적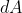 의 투영면에 입사되는 에너지와
의 투영면에 입사되는 에너지와 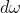 에 입사되는 복사 에너지의 곱이다. 이 관계는 전역 조명 모델의 근간이 되는 출발점이다.
에 입사되는 복사 에너지의 곱이다. 이 관계는 전역 조명 모델의 근간이 되는 출발점이다.
Reference
Philip Dutre, Kavita Bala, Philippe Bekaert, Advanced Global Illumination 2nd Endtion, A.K.Peters, 2006
전역 조명 모델 알고리즘의 궁극적인 목표는 어떤 장면에서 빛의 복사 에너지 방출이 안정적인 상태일 때를 최대한 근사하는 것이다. 지역 조명 모델의 환경광 / 난반사광 / 정반사광만을 사용한 근사식은 특정 상황에서만 정확한 근사식일 뿐이다. 따라서, 보다 정확한 조명을 계산하기 위해서는 아주 미세한 영역에서의 빛의 에너지를 파악해야 한다. 이를 위해서, 플럭스(flux)라고도 불리는 방사 단위를 정의하고
입사되는 에너지의 단위는 와트(Watt)며, 와트는 1 뉴턴의 힘을 1 m 이동하는데 필요한 에너지를 뜻한다. 즉, 위의 표현에서 단위는
다음으로, 특정 표면에서 나오는 빛을 생각할 수 있다. 발광(radiant exitance,
단위는 입사 광도와 동일하다.
이제, 광도(radiance)를 이야기할 수 있다. 광도란 단위 면적에서의, 기하 단위각(solid angle)에 의한 빛의 복사 에너지를 뜻한다. 기하 단위각이란 블로그지기가 임의로 생각한 단어인데, 2차원 평면에서 미분 단위 d는 굴곡이 없지만, 3차원 평면에서의 단위 면적은 굴곡을 포함할 수 있다. 따라서, 3차원 평면에서의 미분 요소 d 2차원 평면에서의 미분 요소 d와 동일한 방법으로 적분할 수 없다. 다음 그림은 이것을 나태낸 것인데, 현실적으로

즉, 특정 위치
즉, 광도는 단위 면적
Reference
Philip Dutre, Kavita Bala, Philippe Bekaert, Advanced Global Illumination 2nd Endtion, A.K.Peters, 2006


