페이스(face)를 하나 생성했을 때, 페이스에 대한 법선 벡터(normal vector)는 여러모로 유용하게 쓰인다. 만약, 페이스에 어떤 변환 행렬 A를 적용했을 때, A의 법선 벡터에도 이 변환 행렬을 적용할 수 있을까? 즉, A의 변환 뒤의 법선 벡터와, 변환 전의 페이스에 A를 적용한 결과가 같을까?
이것은 명확하게 정의되지 않는다. 왜냐하면, 컴퓨터에서의 부동 소수점은 그 자체가 정확하지 않기 때문이다. 단순히 같은 변환을 적용하여 원하는 정도의 정밀도의 값을 얻을 수 있는 경우도 있겠지만, 미묘하게 값이 맞지 않는 경우도 있을 수 있다. 그래서, 단순히 같은 변환을 적용하는 것보다, 변환 행렬이 적용된 페이스의 법선 벡터를 다시 계산하는 것이 좋다.
그러나, 법선 벡터를 재계산하는 것은 비교적 많은 계산 과정이 필요하다. 일반적인 그래픽 시스템에서는 4 * 4 행렬을 사용하며, 곱셈 명령은 비교적 긴 머신 사이클을 필요로 하는 명령이다. 따라서, 페이스 각각에 대해서 이런 계산을 하는 것은 상당히 비싼 작업이다. 그러나, 특정 경우 법선 벡터를 간단하게 계산할 수 있는 좋은 방법이 있다.
문제를 정리해보자. 어떤 페이스를 변환하는 행렬 A가 주어졌을 때, 이 페이스의 법선 벡터를 변환 행렬 A가 적용된 뒤의 페이스와 수직이 되도록 하는 변환 행렬 B는 무엇인가? 즉, n은 페이스의 법선 벡터이고, 페이스의 탄젠트 벡터1 u와 수직일 때 uA · nB = 0을 만족하는 B는 무엇인가? 다음은 B를 구하기 위한 과정을 정리한 것이다.
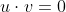
∵ 탄젠트 벡터와 법선 벡터의 유클리드 내적은 0이다.
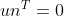
∵ 유클리드 내적이 아닌, 일반적인 행렬의 곱으로 다시 표기해도 결과는 마찬가지이다.
n^T = 0, \; uAA^{-1}n^T = 0)
(A^{-1}n^T) = 0)
((A^{-1}n^T)^T)^T=0)
∵ 전치 행렬을 다시 한번 뒤집으면 자기 자신이 된다.
(n(A^{-1})^T)^T = 0)
∵ 곱으로 이루어진 항에 전치 행렬을 적용할 때는 역순이 된다 :^T = B^TA^T)
^T = 0, \; B=(A^{-1})^T)
즉, 구하고자 하는 행렬 B는 주어진 변환 행렬의 역행렬의 전치 행렬이다. 그런데, A가 직교 행렬(orthogonal matrix)2일 경우, A^T = A^-1의 관계가 있다. 따라서, B = (A^T)^T = A가 된다. 이것은, 법선 벡터를 계산하기 위해 새로운 계산을 할 필요 없이, 그냥 변환 행렬 A를 적용하면 된다는 뜻이다. 즉, 비균등(nonuniform), 또는 쉬어(shear) 변환일 경우 이것을 사용하면 된다. 전치 행렬에 대해서는, 다음을 참조하라. : http://celdee.tistory.com/625
그러나, 위와 같은 변환조차도 때로는 정확하지 않을 수 있다. 그럴 때는 변환 뒤에 법선 벡터를 다시 계산해야만 한다.
Copy From
Frank D. Luna, Introduction to 3D Game Programming with DirectX 10, Wordware Publishing Inc., p184
이것은 명확하게 정의되지 않는다. 왜냐하면, 컴퓨터에서의 부동 소수점은 그 자체가 정확하지 않기 때문이다. 단순히 같은 변환을 적용하여 원하는 정도의 정밀도의 값을 얻을 수 있는 경우도 있겠지만, 미묘하게 값이 맞지 않는 경우도 있을 수 있다. 그래서, 단순히 같은 변환을 적용하는 것보다, 변환 행렬이 적용된 페이스의 법선 벡터를 다시 계산하는 것이 좋다.
그러나, 법선 벡터를 재계산하는 것은 비교적 많은 계산 과정이 필요하다. 일반적인 그래픽 시스템에서는 4 * 4 행렬을 사용하며, 곱셈 명령은 비교적 긴 머신 사이클을 필요로 하는 명령이다. 따라서, 페이스 각각에 대해서 이런 계산을 하는 것은 상당히 비싼 작업이다. 그러나, 특정 경우 법선 벡터를 간단하게 계산할 수 있는 좋은 방법이 있다.
문제를 정리해보자. 어떤 페이스를 변환하는 행렬 A가 주어졌을 때, 이 페이스의 법선 벡터를 변환 행렬 A가 적용된 뒤의 페이스와 수직이 되도록 하는 변환 행렬 B는 무엇인가? 즉, n은 페이스의 법선 벡터이고, 페이스의 탄젠트 벡터1 u와 수직일 때 uA · nB = 0을 만족하는 B는 무엇인가? 다음은 B를 구하기 위한 과정을 정리한 것이다.
∵ 탄젠트 벡터와 법선 벡터의 유클리드 내적은 0이다.
∵ 유클리드 내적이 아닌, 일반적인 행렬의 곱으로 다시 표기해도 결과는 마찬가지이다.
∵ 전치 행렬을 다시 한번 뒤집으면 자기 자신이 된다.
∵ 곱으로 이루어진 항에 전치 행렬을 적용할 때는 역순이 된다 :
즉, 구하고자 하는 행렬 B는 주어진 변환 행렬의 역행렬의 전치 행렬이다. 그런데, A가 직교 행렬(orthogonal matrix)2일 경우, A^T = A^-1의 관계가 있다. 따라서, B = (A^T)^T = A가 된다. 이것은, 법선 벡터를 계산하기 위해 새로운 계산을 할 필요 없이, 그냥 변환 행렬 A를 적용하면 된다는 뜻이다. 즉, 비균등(nonuniform), 또는 쉬어(shear) 변환일 경우 이것을 사용하면 된다. 전치 행렬에 대해서는, 다음을 참조하라. : http://celdee.tistory.com/625
그러나, 위와 같은 변환조차도 때로는 정확하지 않을 수 있다. 그럴 때는 변환 뒤에 법선 벡터를 다시 계산해야만 한다.
Copy From
Frank D. Luna, Introduction to 3D Game Programming with DirectX 10, Wordware Publishing Inc., p184


