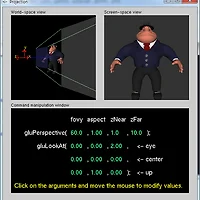
어떤 3D 모델링된 물체를 컴퓨터가 그래픽 시스템을 통해 그린다고 생각해보자. 전통적인 렌더링 파이프라인에서 모델링 정보를 처리하는 응용 단계(application stage)를 거쳐 가상의 공간에서 기하 변환(geometry stage)이 이루어진 뒤, 래스터화 단계(rasterization stage)를 거쳐 최종적으로 장치에 출력된다.
응용 단계에서부터 생각해보자. 어떤 물체를 3D 모델링 소프트웨어를 사용해서 만들어냈다고 하면, 각 정점의 정보는 무엇을 기준으로 한 것일까? 당연히, 물체 자신을 원점을 기준으로 한 것이다. 모델링 소프트웨어가 저장하는 물체의 기하 정보는, 물체 자신의 원점을 기준으로 한 상대적인 각각의 정점의 위치 따위이다. 시점을 기준으로 한 정점의 위치를 저장할 수도 있겠지만, 이렇게되면 시점 위치에 대한 정보도 추가적으로 저장해야 하고, 이 기하 정보를 이용하는 것도 불편하다. 따라서, 기하 정보를 저장한다면 모델링된 물체 자신의 좌표계(로컬 좌표계)를 기준으로 정점의 정보를 저장하는 것이 일반적이다.
자신의 위치를 완전하게 정의한 물체의 정점 정보가 준비되었다면, 그래픽 시스템은 물체를 화면에 표시하기 위해 기하 변환을 적용한다. 기하 변환 과정은 크게 모델뷰 변환(modelview transformation)과 투영 변환(projection transformation), 뷰포트 변환(viewport transformation)으로 구분할 수 있는데, 여기서는 모델뷰 변환에 대해서 이야기해보자.
모델뷰 변환이란, 모델 변환과 뷰 변환의 각각 독립적인 변환을 합친 말인데, 이것은 두 변환이 개념상으로는 구분되어 있지만 사실 동일한 변환이기 때문이다. 그래픽 시스템이 가상의 공간에 어떤 물체를 그린다고 했을 때, 그래픽 시스템을 구현하는 입장에서 생각해보자. 자신의 독립적인 좌표계에서 정의된 물체를 어떻게 전체 공간(world coordinate)에서 그릴 것인가? 만약, 이 물체를 가상의 전체 공간 중 특정한 위치에 배치하지 않았다면, 전체 공간의 좌표계와 물체 공간의 좌표계를 일치시켜 그릴 것이다(서로의 원점을 일치시킨다는 뜻이다). 즉, 그래픽 시스템은 무언가를 그릴 때 전역 좌표계와 로컬 좌표계(물체 자신의 고유한 좌표계)를 동시에 고려하는 것이 아니라, 자신의 전역 좌표계를 로컬 좌표계로 옮긴 다음 그린다. 왜냐하면, 자신의 원점을 기준으로 한 정점 정보를 가지고 있는 물체를 그릴 때 물체의 좌표값 각각을 전역 좌표계와 보정하여 그리는 것보다, 전역 좌표계를 물체 자신의 좌표계 원점, 즉 로컬 좌표계와 일치시켜 그리는 것이 훨씬 단순하고 효율적이기 때문이다. 이 과정을 모델 변환이라고 하는데, 이것은 물체 각각의 로컬 좌표계에서 정의된 물체의 기하 정보를 전역 좌표계에 맞추어 변환하는 과정을 말한다. 사실 그래픽 시스템 입장에서는 전역 좌표를 로컬 좌표에 일치시키기 때문에, 모델 변환을 처음 접한다면 변환 순서가 직관적으로 이해되지 않을 것이다. 그래픽 시스템 구현자 이야기를 꺼낸 것은, 구현자의 입장에서 이 문제를 생각해보는 것이 변환 순서를 직관적으로 이해하는데 훨씬 도움이 되기 때문이다. 또, 물체는 가상의 전체 공간에서 얌전하게만 있는 것이 아니라 크기가 변하기도 하고(scaling), 회전하기도 한다(rotation). 이런 변환 모두 모델 변환에 포함된다.
그러나, 이 가상의 공간에 존재하는 물체를 관찰하기 위해서는 이것으로 충분하지 않다. 이 물체를 관찰하는 시점에 대한 정보가 있어야 이 물체들의 위치 정보를 완전하게 결정할 수 있게 된다. 즉, 시점은 카메라와 동일하다. 카메라를 밀거나 당겨서 물체를 관찰할 수도 있고(이 경우 물체는 확대되거나 축소되어 관찰된다), 카메라를 기울여서 관찰할 수도 있다(이 경우 물체는 회전된 상태로 보이게 된다). 즉, 이런 시점을 반영하는 과정을 뷰 변환이라고 하는데, 사실 이것은 모델 변환과 개념상으로는 구분할 수 있을지 몰라도, 실제로는 모델 변환과 동일하다. 즉, 물체를 자세히 보기 위해 카메라를 미는 것은, 사실 물체를 확대하는 것과 아무런 차이가 없다. 카메라를 기울이는 것도, 물체 자체를 기울인다면 관찰자에게는 동일한 변환으로 보인다. 그래서 많은 그래픽 시스템은 모델 변환과 뷰 변환을 동일하게 취급하여 하나의 변환으로 간주한다.
예를 들어, 모델 변환을 위한 행렬을 M, 뷰 변환을 위한 행렬을 V라 할 때, 전역 좌표계에서 이 변환은 V · M · (object)로 표현된다. 그래픽 시스템은 물체를 그리기 위해 자신의 전역 좌표계와 물체의 로컬 좌표계를 일치시킨 뒤 뷰 변환을 가하는데, V · M은 사실 단일한 하나의 변환으로 표현할 수 있기 때문에, 이 두 변환을 따로 구분하지 않는다.
즉, 모델뷰 변환은 관찰 시점과 그리고자 하는 물체의 로컬 좌표계를 전역 좌표계에 맞추어 변환하는 과정을 뜻하며, 나타내고자 하는 물체를 가상의 공간에 의도한대로 기하 변환을 하는 단계라 할 수 있다. 둘을 명확하게 구분하여 말한다면, 임의의 물체들을 가상의 공간에서 원하는대로 변환하는 과정이 모델 변환이다. 그리고, 이들 물체는 결국 카메라 필름과 같은 뷰평면을 거쳐 보여지는 것이므로, 시점 정보가 반영되어야 한다. 올바른 영상을 얻기 위해서는, 공간의 물체를 시점에 맞추어 변환하거나, 관찰자가 움직여야 한다. 관찰자는 움직일 수 없으므로, 공간 상에 위치한 물체를 시점에 맞추어 변환해야 한다. 여기에 적용되는 변환 행렬이 뷰 변환 행렬이다. 모델 변환, 뷰 변환 후 투영 변환(projection transformation), 뷰포트 변환(viewport transformation)을 거쳐 실제로 보여지는 영상을 얻게 된다.
응용 단계에서부터 생각해보자. 어떤 물체를 3D 모델링 소프트웨어를 사용해서 만들어냈다고 하면, 각 정점의 정보는 무엇을 기준으로 한 것일까? 당연히, 물체 자신을 원점을 기준으로 한 것이다. 모델링 소프트웨어가 저장하는 물체의 기하 정보는, 물체 자신의 원점을 기준으로 한 상대적인 각각의 정점의 위치 따위이다. 시점을 기준으로 한 정점의 위치를 저장할 수도 있겠지만, 이렇게되면 시점 위치에 대한 정보도 추가적으로 저장해야 하고, 이 기하 정보를 이용하는 것도 불편하다. 따라서, 기하 정보를 저장한다면 모델링된 물체 자신의 좌표계(로컬 좌표계)를 기준으로 정점의 정보를 저장하는 것이 일반적이다.
자신의 위치를 완전하게 정의한 물체의 정점 정보가 준비되었다면, 그래픽 시스템은 물체를 화면에 표시하기 위해 기하 변환을 적용한다. 기하 변환 과정은 크게 모델뷰 변환(modelview transformation)과 투영 변환(projection transformation), 뷰포트 변환(viewport transformation)으로 구분할 수 있는데, 여기서는 모델뷰 변환에 대해서 이야기해보자.
모델뷰 변환이란, 모델 변환과 뷰 변환의 각각 독립적인 변환을 합친 말인데, 이것은 두 변환이 개념상으로는 구분되어 있지만 사실 동일한 변환이기 때문이다. 그래픽 시스템이 가상의 공간에 어떤 물체를 그린다고 했을 때, 그래픽 시스템을 구현하는 입장에서 생각해보자. 자신의 독립적인 좌표계에서 정의된 물체를 어떻게 전체 공간(world coordinate)에서 그릴 것인가? 만약, 이 물체를 가상의 전체 공간 중 특정한 위치에 배치하지 않았다면, 전체 공간의 좌표계와 물체 공간의 좌표계를 일치시켜 그릴 것이다(서로의 원점을 일치시킨다는 뜻이다). 즉, 그래픽 시스템은 무언가를 그릴 때 전역 좌표계와 로컬 좌표계(물체 자신의 고유한 좌표계)를 동시에 고려하는 것이 아니라, 자신의 전역 좌표계를 로컬 좌표계로 옮긴 다음 그린다. 왜냐하면, 자신의 원점을 기준으로 한 정점 정보를 가지고 있는 물체를 그릴 때 물체의 좌표값 각각을 전역 좌표계와 보정하여 그리는 것보다, 전역 좌표계를 물체 자신의 좌표계 원점, 즉 로컬 좌표계와 일치시켜 그리는 것이 훨씬 단순하고 효율적이기 때문이다. 이 과정을 모델 변환이라고 하는데, 이것은 물체 각각의 로컬 좌표계에서 정의된 물체의 기하 정보를 전역 좌표계에 맞추어 변환하는 과정을 말한다. 사실 그래픽 시스템 입장에서는 전역 좌표를 로컬 좌표에 일치시키기 때문에, 모델 변환을 처음 접한다면 변환 순서가 직관적으로 이해되지 않을 것이다. 그래픽 시스템 구현자 이야기를 꺼낸 것은, 구현자의 입장에서 이 문제를 생각해보는 것이 변환 순서를 직관적으로 이해하는데 훨씬 도움이 되기 때문이다. 또, 물체는 가상의 전체 공간에서 얌전하게만 있는 것이 아니라 크기가 변하기도 하고(scaling), 회전하기도 한다(rotation). 이런 변환 모두 모델 변환에 포함된다.
그러나, 이 가상의 공간에 존재하는 물체를 관찰하기 위해서는 이것으로 충분하지 않다. 이 물체를 관찰하는 시점에 대한 정보가 있어야 이 물체들의 위치 정보를 완전하게 결정할 수 있게 된다. 즉, 시점은 카메라와 동일하다. 카메라를 밀거나 당겨서 물체를 관찰할 수도 있고(이 경우 물체는 확대되거나 축소되어 관찰된다), 카메라를 기울여서 관찰할 수도 있다(이 경우 물체는 회전된 상태로 보이게 된다). 즉, 이런 시점을 반영하는 과정을 뷰 변환이라고 하는데, 사실 이것은 모델 변환과 개념상으로는 구분할 수 있을지 몰라도, 실제로는 모델 변환과 동일하다. 즉, 물체를 자세히 보기 위해 카메라를 미는 것은, 사실 물체를 확대하는 것과 아무런 차이가 없다. 카메라를 기울이는 것도, 물체 자체를 기울인다면 관찰자에게는 동일한 변환으로 보인다. 그래서 많은 그래픽 시스템은 모델 변환과 뷰 변환을 동일하게 취급하여 하나의 변환으로 간주한다.
예를 들어, 모델 변환을 위한 행렬을 M, 뷰 변환을 위한 행렬을 V라 할 때, 전역 좌표계에서 이 변환은 V · M · (object)로 표현된다. 그래픽 시스템은 물체를 그리기 위해 자신의 전역 좌표계와 물체의 로컬 좌표계를 일치시킨 뒤 뷰 변환을 가하는데, V · M은 사실 단일한 하나의 변환으로 표현할 수 있기 때문에, 이 두 변환을 따로 구분하지 않는다.
즉, 모델뷰 변환은 관찰 시점과 그리고자 하는 물체의 로컬 좌표계를 전역 좌표계에 맞추어 변환하는 과정을 뜻하며, 나타내고자 하는 물체를 가상의 공간에 의도한대로 기하 변환을 하는 단계라 할 수 있다. 둘을 명확하게 구분하여 말한다면, 임의의 물체들을 가상의 공간에서 원하는대로 변환하는 과정이 모델 변환이다. 그리고, 이들 물체는 결국 카메라 필름과 같은 뷰평면을 거쳐 보여지는 것이므로, 시점 정보가 반영되어야 한다. 올바른 영상을 얻기 위해서는, 공간의 물체를 시점에 맞추어 변환하거나, 관찰자가 움직여야 한다. 관찰자는 움직일 수 없으므로, 공간 상에 위치한 물체를 시점에 맞추어 변환해야 한다. 여기에 적용되는 변환 행렬이 뷰 변환 행렬이다. 모델 변환, 뷰 변환 후 투영 변환(projection transformation), 뷰포트 변환(viewport transformation)을 거쳐 실제로 보여지는 영상을 얻게 된다.